Hey guys!!
This simple function will return an object's velocity right after colliding with another object.
Very useful for games or (Newtonian) physics projects in general.
PostCollisionVelocity
Remember, you must apply this formula for each axis separately.
See it in action!
Consider two particles, denoted by subscripts 1 and 2. Let m1 and m2 be the masses, u1 and u2 the velocities before collision, and v1 and v2 the velocities after collision.
The conservation of the total momentum demands that the total momentum before the collision is the same as the total momentum after the collision, and is expressed by the equation
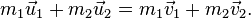
These equations may be solved directly to find vi when ui are known or vice versa.
Solving these simultaneous equations for vi we get:
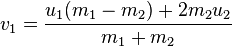 _______
_______
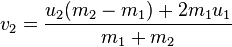
Sources:
Usage example:


(Edits: Better usage example and more detailed information.)
This simple function will return an object's velocity right after colliding with another object.
Very useful for games or (Newtonian) physics projects in general.
PostCollisionVelocity
B4X:
'Given the Conservation of Momentum formula (m1*u1)+(m2*u2) = (m1*v1)+(m2*v2),
'we're able to calculate an object's post collision velocity.
'
'u1: ObjectA pre-collision velocity, u2: ObjectB pre-collision velocity, m1: ObjectA mass in kg, m2: ObjectB mass in kg.
'CoR: Coefficient of Restitution, a value between 0.00(0) and 1.00(0) where 1 represents a perfectly elastic collision.
Sub PostCollisionVelocity(u1 As Double, u2 As Double, m1 As Double, m2 As Double, CoR As Double) As Double
Dim v1 = ((u1 * (m1 - m2)) + (2 * m2 * u2)) / (m1 + m2) As Double
Return v1 * CoR
End SubRemember, you must apply this formula for each axis separately.
See it in action!
Consider two particles, denoted by subscripts 1 and 2. Let m1 and m2 be the masses, u1 and u2 the velocities before collision, and v1 and v2 the velocities after collision.
The conservation of the total momentum demands that the total momentum before the collision is the same as the total momentum after the collision, and is expressed by the equation
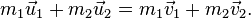
These equations may be solved directly to find vi when ui are known or vice versa.
Solving these simultaneous equations for vi we get:
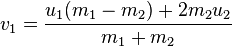
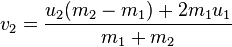
Sources:
Elastic collision: https://en.wikipedia.org/wiki/Elastic_collision
Conservation of Momentum: http://www.physicsclassroom.com/class/momentum/Lesson-2/Momentum-Conservation-Principle
Coefficient of Restitution: http://hypertextbook.com/facts/2006/restitution.shtml
Conservation of Momentum: http://www.physicsclassroom.com/class/momentum/Lesson-2/Momentum-Conservation-Principle
Coefficient of Restitution: http://hypertextbook.com/facts/2006/restitution.shtml
Usage example:

B4X:
'For all collisions in this example, we'll imagine a CoR of 80%
...
Ball.Mass = 10
Wall.Mass = 99999
Floor.Mass = 99999
Ball.VelocityX = 50
Ball.VelocityY = 20
Wall.VelocityX = 0
Wall.VelocityY = 0
Floor.VelocityX = 0
Floor.VelocityY = 0
...
'Collision detection: the Ball hits the Wall from the left (x-axis).
If (Ball.Left + Ball.Width) > Wall.Left Then
Ball.Left = (Wall.Left - Ball.Width)
Ball.VelocityX = PostCollisionVelocity(Ball.VelocityX, Wall.VelocityX, Ball.Mass, Wall.Mass, 0.8)
End If
'Collision detection: the Ball hits the Wall from the right (x-axis).
If Ball.Left < (Wall.Left + Wall.Width) Then
Ball.Left = (Wall.Left + Wall.Width)
Ball.VelocityX = PostCollisionVelocity(Ball.VelocityX, Wall.VelocityX, Ball.Mass, Wall.Mass, 0.8)
End If
'Collision detection: the Ball hits the top of the Wall (y-axis).
If (Ball.Top + Ball.Height) > Wall.Top Then
Ball.Top = (Wall.Top - Ball.Height)
Ball.VelocityY = PostCollisionVelocity(Ball.VelocityY, Wall.VelocityY, Ball.Mass, Wall.Mass, 0.8)
End If
'Collision detection: the Ball hits the Floor (y-axis).
If (Ball.Top + Ball.Height) > Floor.Top Then
Ball.Top = (Floor.Top - Ball.Height)
Ball.VelocityY = PostCollisionVelocity(Ball.VelocityY, Floor.VelocityY, Ball.Mass, Wall.Mass, 0.8)
End If
'Apply Gravity
Ball.VelocityY = Ball.VelocityY + Gravity
'Update Ball Position
Ball.Left = Ball.Left + Ball.VelocityX
Ball.Top = Ball.Top + Ball.VelocityY
...
(Edits: Better usage example and more detailed information.)
Last edited:
