Android Question Get an angle between 2 lines

[ilan]

hi

i would like to rotate a polygon around his center.
i have already the formula for the center point my problem is how to get the angle

so what i do now is when i touch the screen i create a vector (polygon center (x,y)) and the touch x,y
so i have 1 line and this line is 0 angle (its the starting point) now when i move my finger i create everytime a new line (polygon center) and the new x,y and i want to rotate the polygon with the angle between both lines

i tried several formulas i found in the web but nothing gave me the result i wanted
i also found here something but still its not turning correctly. i get to a point where it turns back
(https://www.b4x.com/android/forum/threads/find-angle-for-two-drawlines.13127/#content)

does anyone can help me please?

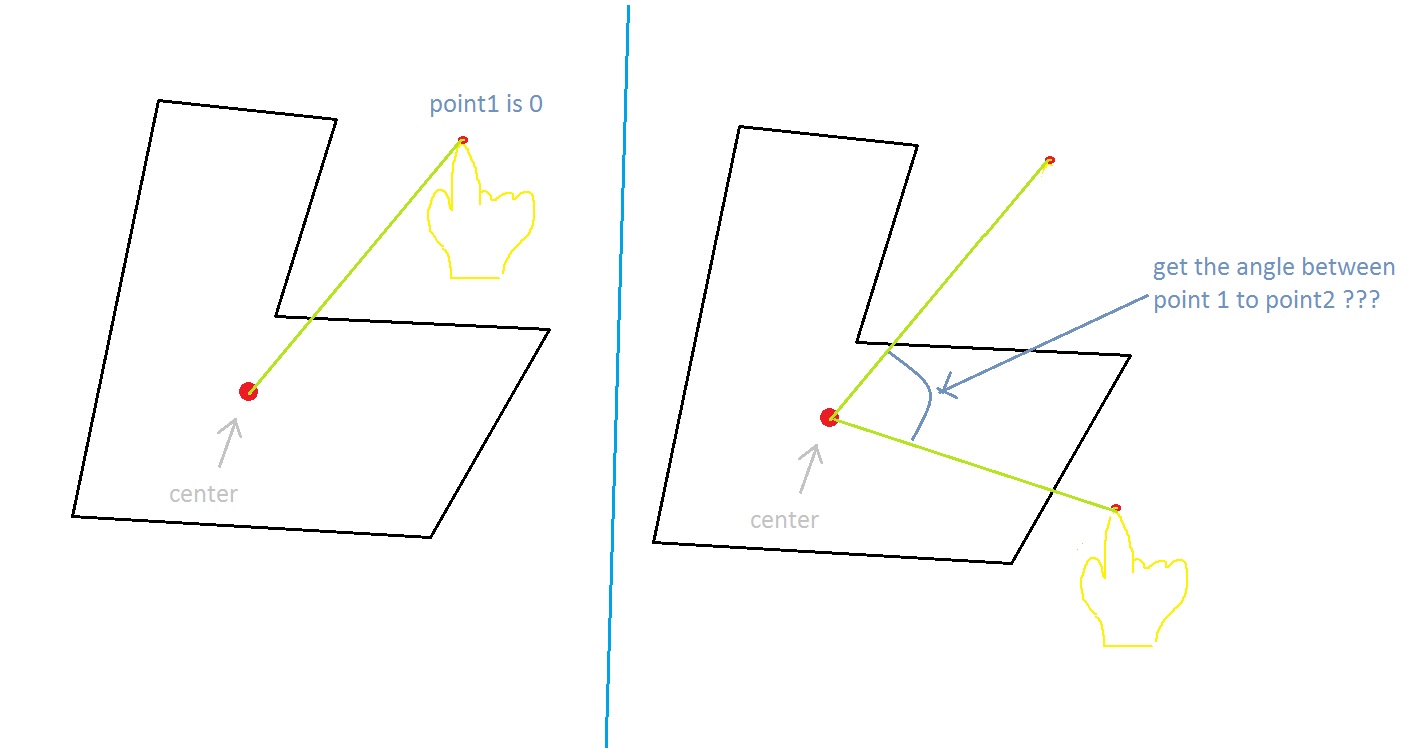
the polygon center is the first point for both vectors! (like in the image)

 

[udg]

Hi Ilan,

I may recall it wrong so please verify it on a math book.
Having two straight lines expressed as ax+by+c=0, you first compute the angular coefficient of each as m=-a/b.
Now you have mr and ms as the two coefficients and can apply the following:
tan(alfa) = absolute value of (mr-ms)/1+mr * ms
and finally alfa = arctan(tan(alfa))
where tan(alfa) is the tangent of angle alfa (the acute one between the initial straight lines).

Again, it could be wrong..it's a long time I don't practice geometry..eheh

 

[ilan]

Hi Ilan,

I may recall it wrong so please verify it on a math book.
Having two straight lines expressed as ax+by+c=0, you first compute the angular coefficient of each as m=-a/b.
Now you have mr and ms as the two coefficients and can apply the following:
tan(alfa) = absolute value of (mr-ms)/1+mr * ms
and finally alfa = arctan(tan(alfa))
where tan(alfa) is the tangent of angle alfa (the acute one between the initial straight lines).

Again, it could be wrong..it's a long time I don't practice geometry..eheh

thanx for your response but i dont understand what is whats

if those are my values how would look the formula to get the angle?

thankx you

 

[udg]

Hi Ilan,

your straight lines respectively have equation:
y= (-5/4) x --> (-5/4) x -y = 0; so referring to ax+by+c=0 you have a=-5/4, b=-1, c=0
y = (1/6) x --> (1/6) x -y = 0; so referring to ax+by+c=0 you have a=1/6, b=-1, c=0
that leads to
mr = - (-5/4) / -1 ; mr = -5/4
ms = - (1/6) / -1; ms = 1/6
tan(alfa) = absolute value of (mr-ms)/1+mr * ms
tan(alfa) = absolute((-5/4-1/6)/ (1+ (-5/4 * 1/6))) = absolute ((-17/12) / (1- 5/24)) = absolute(-17/12 * 24/19)= 34/19
alfa = arctan(34/19)

udg

 

[ilan]

thanx a lot @udg i will try it out

 

[ilan]

@udg you are a genius!!
the formula is working!!! thank you so much i will now need to see if it works in my app too

Code:

Sub Process_Globals
    Private fx As JFX
    Private MainForm As Form
    Type vector(x As Float, y As Float)
End Sub

'....

Sub calcdegree
    Dim point1, point2 As vector
    point1.x = 40
    point1.y = -50
    point2.x = 60
    point2.y = 10
    Log(getangle(point1,point2))  
End Sub

Sub getangle (p1 As vector, p2 As vector) As Double
    Dim mr,ms,tan_alfa As Double
    mr = (p1.y/p1.x)/-1
    ms = (p2.y/p2.x)/-1
    tan_alfa = Abs((mr-ms)/(1+(mr*ms)))
    Return ATanD(tan_alfa)
End Sub

 

[ilan]

a little think i just saw when the result is over 90 i will get the degress for the second angle like

Sub calcdegree
    Dim point1, point2 As vector
    point1.x = 40
    point1.y = -50
    point2.x = 5
    point2.y = 30
    Log(getangle(point1,point2))  
End Sub

Sub getangle (p1 As vector, p2 As vector) As Double
    Dim mr,ms,tan_alfa As Double
    mr = (p1.y/p1.x)/-1
    ms = (p2.y/p2.x)/-1
    tan_alfa = Abs((mr-ms)/(1+(mr*ms)))
    Return ATanD(tan_alfa)
End Sub

i am getting = 48.12213046211571
but i want = 131.878

 

[JordiCP]

I think atan2 takes quadrants into acocunt

Also, depending in the quadrant you are you can do 180-angle

 

[ilan]

I think atan2 takes quadrants into acocunt

Also, depending in the quadrant you are you can do 180-angle

but Atan2 is asking for x and y

 

[ilan]

ok this seems to work

Sub calcdegree
    Dim point1, point2 As vector
    point1.x = 40
    point1.y = -50
    point2.x = 5
    point2.y = 30
    Log(getangle(point1,point2))
End Sub

Sub getangle (p1 As vector, p2 As vector) As Double
    Dim mr,ms As Double
    mr = (p1.y/p1.x)/-1
    ms = (p2.y/p2.x)/-1
    Return ATan2D((mr-ms),(1+(mr*ms)))
End Sub

will need to make more tests

 

[ilan]

ok i dont know why but x 0 are not calculated correctly

this formula works

Sub calcdegree
    Dim point1, point2 As vector
    point1.x = 40
    point1.y = -50
    point2.x = 5
    point2.y = 30
    Log(getangle(point1,point2))
End Sub

Sub getangle (p1 As vector, p2 As vector) As Double
    Dim mr,ms As Double
    mr = (p1.y/p1.x)/-1
    ms = (p2.y/p2.x)/-1
    Return ATan2D((mr-ms),(1+(mr*ms)))
End Sub

but not with x = 0 values (if i use x = 0.0001) i get correct answer but x = 0 wrong

why??

 

[JordiCP]

When x=0, depending on the atan2 implementation, it will give undefined since atan2(y,x) is basically atan(y/x)

x=0, y>0 --> atan2(y,x)=cPI/2
x=0, y<0 --> atan2(y,x)=-cPI/2

 

[udg]

One note: I assumed the polygon's center as point(0,0) so the equations given for those two straight lines.

The general rule for a straight line between points (x1,y1) and (x2,y2), where x1<>x2 and y1<>y2, is:

(y-y1) / (y2-y1) = (x-x1) / (x2-x1)

Assuming x1 = 0 and y1=0 (your polygon's center) gave the equations in post #4.
One more note: if the two points have y1=y2 then the equation for the straight line becomes y = y1; if the two points have x1=x2 then the equation becomes x=x1

A final note: I'm glad that after so many years I recalled it right ..and that it worked for you!

udg

 

[ilan]

if the polygon center is not 0,0 how should my code look like?

 

[ilan]

wait wait wait i think i was wrong from the beginning

the polygon center is not relevant

what i need is only the angle between the first point and second point and then i will add that angle to the polygon rotation


so the real center is also the first point because if i touch the screen and get the first point and store it as a variable

then moving on the x axis start creating the second point on every move but if i stay on the y axis and just move on the x axis the polygon should not rotate

if the center of both vectors would be the center of the polygon then moving on the x axis would rotate the polygon because an angle was created and thats wrong

see pic:

the polygon should not rotate in such action so the center cannot be the polygon center

actually in need this formula for my new game (Power Blocks) and now i rotate the polygon by just moving right/left and adding the difference between x1 to x2
but i would like to give a better filling of rotating the polygon by making a circular movement on the screen and like this rotate the polygon would be more realistic then it is now

i guess this task would be to complicated to do...

 

[udg]

Given A (x1,y1), B (x2,y2) and PCenter (x0,y0)

I would modify mr and ms like:

mr = (x1 -x0) / (y1-y0)
ms = (x2-x0) / (y2 -y0)

This will be independent from the (0,0) point.

 

[ilan]

like this @udg ?

Sub calcdegree
    Dim point1, point2, center As vector
    center.x = 50
    center.y = 50
    point1.x = 40
    point1.y = -50
    point2.x = 0
    point2.y = 30
    Log(getangle(point1,point2,center)) 
End Sub

Sub getangle (p1 As vector, p2 As vector,p0 As vector) As Double
    Dim mr,ms As Double
    mr = (p1.x-p0.x) / (p1.y-p0.y)
    ms = (p2.x-p0.x) / (p2.y-p0.y)
    Return ATan2D((mr-ms),(1+(mr*ms)))
End Sub

 

[udg]

if p0 is the point (x0,y0) in your drawing, yes.
I simply redetermined the angular cofficient of straight line r (the one between p0 and p1) and s (the one between p0 and p2) where p0 is not more the (0,0) point in the coordinate system.

 

[ilan]

hi @udg sorry if i bother you again

i tried and tried and tried but it seems like i am not getting the correct result

please check the including b4j project, thanx

 

[udg]

Hi Ilan, no problem.
Today I have access to my dev PC so I can try what until now "ran" only in my mind.. eheh
And a sheet of paper and a pencil will be of great help too.