[SOLVED] See attached project files.
PS: Here's the difference between Flood() and Fill(): https://www.diffchecker.com/OO65W6Jm
Initial post:
This question is aimed at @Informatix or anyone who's able to help.
Given a true/false matrix, as shown below, where black is true and transparent is false, I believe I could use a path finding algorithm for simulating "filling the gaps with water", given the entry point shown in red.
The question is, how can we achieve this?
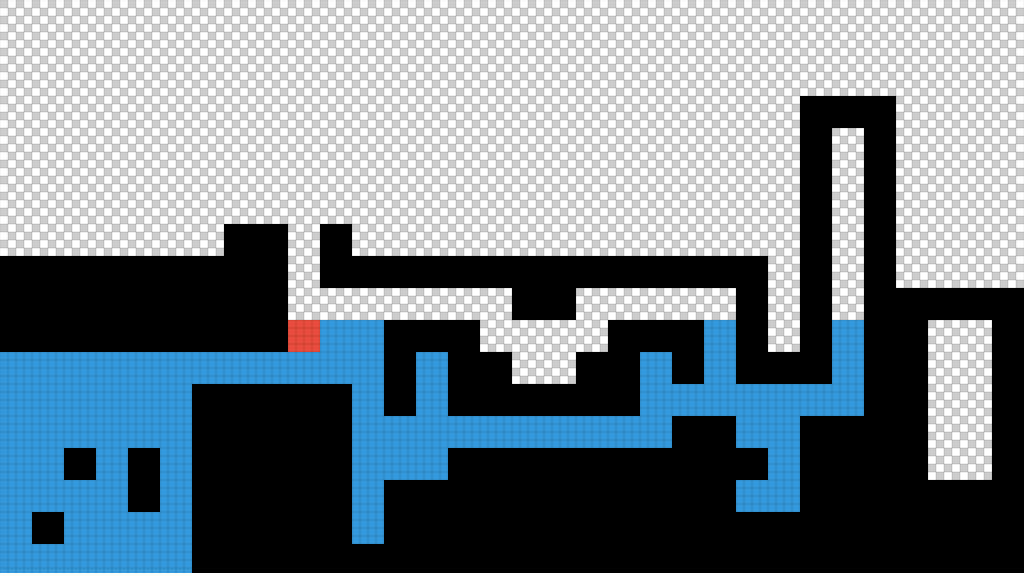
Expected result
B4X:
'Static code module
Private Sub Process_Globals
Private fx As JFX
Private stack As List
End Sub
Public Sub Initialize
stack.Initialize
End Sub
Public Sub Fill(value As Int, x As Int, y As Int, grid As Grid)
Dim top = y As Int
Dim matrix(,) = grid.matrix As Int
If value = matrix(x, y) Then Return
'--------------------------------------------------------------
stack.Clear
Dim x1 As Int
Dim spanAbove, spanBelow As Boolean
'--------------------------------------------------------------
stack.Add(Array As Int(x, y))
'--------------------------------------------------------------
Dim p() As Int
Do While (stack.Size > 0)
p = stack.Get(stack.Size - 1)
x = p(0) : y = p(1) : stack.RemoveAt(stack.Size - 1)
'----------------------------------------------------------
x1 = x : Do While (x1 >= 0 And matrix(x1, y) == 0) : x1 = x1 - 1 : Loop
'----------------------------------------------------------
x1 = x1 + 1 : spanAbove = False : spanBelow = False
'----------------------------------------------------------
Do While (x1 < grid.sizeX And matrix(x1, y) = 0)
matrix(x1, y) = value
'------------------------------------------------------
If (spanAbove = False And y > top And matrix(x1, y - 1) = 0) Then
spanAbove = True : stack.Add(Array As Int(x1, y - 1))
Else If (spanAbove = True And y > top And matrix(x1, y - 1) > 0) Then
spanAbove = False
End If
'------------------------------------------------------
If (spanBelow = False And y < grid.sizeY - 1 And matrix(x1, y + 1) = 0) Then
spanBelow = True : stack.Add(Array As Int(x1, y + 1))
Else If (spanBelow And y < grid.sizeY - 1 And matrix(x1, y + 1) > 0) Then
spanBelow = False
End If
'------------------------------------------------------
x1 = x1 + 1
Loop
Loop
End Sub
Public Sub Flood(value As Int, x As Int, y As Int, grid As Grid)
Dim matrix(,) = grid.matrix As Int
If value = matrix(x, y) Then Return
'--------------------------------------------------------------
stack.Clear
Dim x1 As Int
Dim spanAbove, spanBelow As Boolean
'--------------------------------------------------------------
stack.Add(Array As Int(x, y))
'--------------------------------------------------------------
Dim p() As Int
Do While (stack.Size > 0)
p = stack.Get(stack.Size - 1)
x = p(0) : y = p(1) : stack.RemoveAt(stack.Size - 1)
'----------------------------------------------------------
x1 = x : Do While (x1 >= 0 And matrix(x1, y) == 0) : x1 = x1 - 1 : Loop
'----------------------------------------------------------
x1 = x1 + 1 : spanAbove = False : spanBelow = False
'----------------------------------------------------------
Do While (x1 < grid.sizeX And matrix(x1, y) = 0)
matrix(x1, y) = value
'------------------------------------------------------
If (spanAbove = False And y > 0 And matrix(x1, y - 1) = 0) Then
spanAbove = True : stack.Add(Array As Int(x1, y - 1))
Else If (spanAbove = True And y > 0 And matrix(x1, y - 1) > 0) Then
spanAbove = False
End If
'------------------------------------------------------
If (spanBelow = False And y < grid.sizeY - 1 And matrix(x1, y + 1) = 0) Then
spanBelow = True : stack.Add(Array As Int(x1, y + 1))
Else If (spanBelow And y < grid.sizeY - 1 And matrix(x1, y + 1) > 0) Then
spanBelow = False
End If
'------------------------------------------------------
x1 = x1 + 1
Loop
Loop
End SubInitial post:
This question is aimed at @Informatix or anyone who's able to help.
Given a true/false matrix, as shown below, where black is true and transparent is false, I believe I could use a path finding algorithm for simulating "filling the gaps with water", given the entry point shown in red.
The question is, how can we achieve this?
Expected result
Attachments
Last edited:
