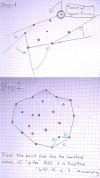
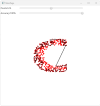
#Region Project Attributes
#MainFormWidth: 600
#MainFormHeight: 600
#End Region
Sub Process_Globals
Private fx As JFX
Private MainForm As Form
Private xui As XUI
Dim pointList As List
Private cv As Canvas
Dim nativeMe As JavaObject
End Sub
Sub AppStart (Form1 As Form, Args() As String)
MainForm = Form1
MainForm.RootPane.LoadLayout("Layout1")
MainForm.Show
pointList.Initialize
nativeMe = Me
Dim aa As JavaObject
For i = 0 To 200
Dim x As Double = Rnd(50, 520).As(Double)
Dim y As Double = Rnd(200,400).As(Double)
aa.InitializeNewInstance("b4j.example.main.Point", Array(x, y))
pointList.Add(aa)
cv.DrawCircle(x, y, 2, fx.Colors.Black, True, 0)
Next
Dim k As Int = 3
Dim returnlist As List
returnlist.Initialize
returnlist = nativeMe.RunMethod("calculateConcaveHull", Array(pointList, k))
Dim prevX, prevY As Double
For i = 0 To returnlist.Size - 1
Dim dd(2) As String = Regex.Split(" ", returnlist.Get(i))
Dim bbx As Double = dd(0).Replace("(", "")
Dim bby As Double = dd(1).Replace(")", "")
cv.DrawCircle(bbx, bby, 2, fx.Colors.Blue, True, 0)
If i = 0 Then
prevX = bbx
prevY = bby
End If
If i > 0 Then
cv.Drawline(prevX, prevY, bbx, bby, fx.Colors.Red, 2)
End If
prevX = bbx
prevY = bby
Next
Log("FINISH")
End Sub
#If Java
import javafx.util.Pair;
import java.util.*;
/**
* ConcaveHull.java - 14/10/16
*
* @author Udo Schlegel - Udo.3.Schlegel(at)uni-konstanz.de
* @version 1.0
*
* This is an implementation of the algorithm described by Adriano Moreira and Maribel Yasmina Santos:
* CONCAVE HULL: A K-NEAREST NEIGHBOURS APPROACH FOR THE COMPUTATION OF THE REGION OCCUPIED BY A SET OF POINTS.
* GRAPP 2007 - International Conference on Computer Graphics Theory and Applications; pp 61-68.
*
* https://repositorium.sdum.uminho.pt/bitstream/1822/6429/1/ConcaveHull_ACM_MYS.pdf
*
* With help from https://github.com/detlevn/QGIS-ConcaveHull-Plugin/blob/master/concavehull.py
*/
public static class Point {
private final Double x;
private final Double y;
public Point(Double x, Double y) {
this.x = x;
this.y = y;
}
public Double getX() {
return x;
}
public Double getY() {
return y;
}
public String toString() {
return "(" + x + " " + y + ")";
}
@Override
public boolean equals(Object obj) {
if (obj instanceof Point) {
if (x.equals(((Point) obj).getX()) && y.equals(((Point) obj).getY())) {
return true;
} else {
return false;
}
} else {
return false;
}
}
@Override
public int hashCode() {
// http://stackoverflow.com/questions/22826326/good-hashcode-function-for-2d-coordinates
// http://www.cs.upc.edu/~alvarez/calculabilitat/enumerabilitat.pdf
int tmp = (int) (y + ((x + 1) / 2));
return Math.abs((int) (x + (tmp * tmp)));
}
}
private static Double euclideanDistance(Point a, Point b) {
return Math.sqrt(Math.pow(a.getX() - b.getX(), 2) + Math.pow(a.getY() - b.getY(), 2));
}
private static ArrayList<Point> kNearestNeighbors(ArrayList<Point> l, Point q, Integer k) {
ArrayList<Pair<Double, Point>> nearestList = new ArrayList<>();
for (Point o : l) {
nearestList.add(new Pair<>(euclideanDistance(q, o), o));
}
Collections.sort(nearestList, new Comparator<Pair<Double, Point>>() {
@Override
public int compare(Pair<Double, Point> o1, Pair<Double, Point> o2) {
return o1.getKey().compareTo(o2.getKey());
}
});
ArrayList<Point> result = new ArrayList<>();
for (int i = 0; i < Math.min(k, nearestList.size()); i++) {
result.add(nearestList.get(i).getValue());
}
return result;
}
private static Point findMinYPoint(ArrayList<Point> l) {
Collections.sort(l, new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
return o1.getY().compareTo(o2.getY());
}
});
return l.get(0);
}
private static Double calculateAngle(Point o1, Point o2) {
return Math.atan2(o2.getY() - o1.getY(), o2.getX() - o1.getX());
}
private static Double angleDifference(Double a1, Double a2) {
// calculate angle difference in clockwise directions as radians
if ((a1 > 0 && a2 >= 0) && a1 > a2) {
return Math.abs(a1 - a2);
} else if ((a1 >= 0 && a2 > 0) && a1 < a2) {
return 2 * Math.PI + a1 - a2;
} else if ((a1 < 0 && a2 <= 0) && a1 < a2) {
return 2 * Math.PI + a1 + Math.abs(a2);
} else if ((a1 <= 0 && a2 < 0) && a1 > a2) {
return Math.abs(a1 - a2);
} else if (a1 <= 0 && 0 < a2) {
return 2 * Math.PI + a1 - a2;
} else if (a1 >= 0 && 0 >= a2) {
return a1 + Math.abs(a2);
} else {
return 0.0;
}
}
private static ArrayList<Point> sortByAngle(ArrayList<Point> l, Point q, Double a) {
// Sort by angle descending
Collections.sort(l, new Comparator<Point>() {
@Override
public int compare(final Point o1, final Point o2) {
Double a1 = angleDifference(a, calculateAngle(q, o1));
Double a2 = angleDifference(a, calculateAngle(q, o2));
return a2.compareTo(a1);
}
});
return l;
}
private static Boolean intersect(Point l1p1, Point l1p2, Point l2p1, Point l2p2) {
// calculate part equations for line-line intersection
Double a1 = l1p2.getY() - l1p1.getY();
Double b1 = l1p1.getX() - l1p2.getX();
Double c1 = a1 * l1p1.getX() + b1 * l1p1.getY();
Double a2 = l2p2.getY() - l2p1.getY();
Double b2 = l2p1.getX() - l2p2.getX();
Double c2 = a2 * l2p1.getX() + b2 * l2p1.getY();
// calculate the divisor
Double tmp = (a1 * b2 - a2 * b1);
// calculate intersection point x coordinate
Double pX = (c1 * b2 - c2 * b1) / tmp;
// check if intersection x coordinate lies in line line segment
if ((pX > l1p1.getX() && pX > l1p2.getX()) || (pX > l2p1.getX() && pX > l2p2.getX())
|| (pX < l1p1.getX() && pX < l1p2.getX()) || (pX < l2p1.getX() && pX < l2p2.getX())) {
return false;
}
// calculate intersection point y coordinate
Double pY = (a1 * c2 - a2 * c1) / tmp;
// check if intersection y coordinate lies in line line segment
if ((pY > l1p1.getY() && pY > l1p2.getY()) || (pY > l2p1.getY() && pY > l2p2.getY())
|| (pY < l1p1.getY() && pY < l1p2.getY()) || (pY < l2p1.getY() && pY < l2p2.getY())) {
return false;
}
return true;
}
private static boolean pointInPolygon(Point p, ArrayList<Point> pp) {
boolean result = false;
for (int i = 0, j = pp.size() - 1; i < pp.size(); j = i++) {
if ((pp.get(i).getY() > p.getY()) != (pp.get(j).getY() > p.getY()) &&
(p.getX() < (pp.get(j).getX() - pp.get(i).getX()) * (p.getY() - pp.get(i).getY()) / (pp.get(j).getY() - pp.get(i).getY()) + pp.get(i).getX())) {
result = !result;
}
}
return result;
}
public static ArrayList<Point> calculateConcaveHull(ArrayList<Point> pointArrayList, Integer k) {
// the resulting concave hull
ArrayList<Point> concaveHull = new ArrayList<>();
// optional remove duplicates
HashSet<Point> set = new HashSet<>(pointArrayList);
ArrayList<Point> pointArraySet = new ArrayList<>(set);
// k has to be greater than 3 to execute the algorithm
Integer kk = Math.max(k, 3);
// return Points if already Concave Hull
if (pointArraySet.size() < 3) {
return pointArraySet;
}
// make sure that k neighbors can be found
kk = Math.min(kk, pointArraySet.size() - 1);
// find first point and remove from point list
Point firstPoint = findMinYPoint(pointArraySet);
concaveHull.add(firstPoint);
Point currentPoint = firstPoint;
pointArraySet.remove(firstPoint);
Double previousAngle = 0.0;
Integer step = 2;
while ((currentPoint != firstPoint || step == 2) && pointArraySet.size() > 0) {
// after 3 steps add first point to dataset, otherwise hull cannot be closed
if (step == 5) {
pointArraySet.add(firstPoint);
}
// get k nearest neighbors of current point
ArrayList<Point> kNearestPoints = kNearestNeighbors(pointArraySet, currentPoint, kk);
// sort points by angle clockwise
ArrayList<Point> clockwisePoints = sortByAngle(kNearestPoints, currentPoint, previousAngle);
// check if clockwise angle nearest neighbors are candidates for concave hull
Boolean its = true;
int i = -1;
while (its && i < clockwisePoints.size() - 1) {
i++;
int lastPoint = 0;
if (clockwisePoints.get(i) == firstPoint) {
lastPoint = 1;
}
// check if possible new concave hull point intersects with others
int j = 2;
its = false;
while (!its && j < concaveHull.size() - lastPoint) {
its = intersect(concaveHull.get(step - 2), clockwisePoints.get(i), concaveHull.get(step - 2 - j), concaveHull.get(step - 1 - j));
j++;
}
}
// if there is no candidate increase k - try again
if (its) {
return calculateConcaveHull(pointArrayList, k + 1);
}
// add candidate to concave hull and remove from dataset
currentPoint = clockwisePoints.get(i);
concaveHull.add(currentPoint);
pointArraySet.remove(currentPoint);
// calculate last angle of the concave hull line
previousAngle = calculateAngle(concaveHull.get(step - 1), concaveHull.get(step - 2));
step++;
}
// Check if all points are contained in the concave hull
Boolean insideCheck = true;
int i = pointArraySet.size() - 1;
while (insideCheck && i > 0) {
insideCheck = pointInPolygon(pointArraySet.get(i), concaveHull);
i--;
}
// if not all points inside - try again
if (!insideCheck) {
return calculateConcaveHull(pointArrayList, k + 1);
} else {
return concaveHull;
}
}
#End If